前回「応用ができなくて困ってしまう」子どもの話１では、課題を繰り返しやらせても、意味がわからないで形だけまねしてしまうと、応用ができなくなってしまうんだ、という話を書きました。

それは「こういう風にやらなければいけない」ではなくて、「どうしてこういう風にするのか？」という理由を理解できているかどうか、ということでもあります。その理由の理解が伴ってこないと、応用が効かないので、結局ひとつひとつ答えを丸暗記するしかなくなるわけですね。

もう少し例を重ねてみましょう。

昔、とっても勉強が苦手な中学三年生たちに数学を教えたときのことです。「３-５は？」と聞くと、「８！」と明るく答えてくれたりしていた、そんな生徒たちでした。意味が分かってないので、引き算と足し算が混乱しちう。負の数などイメージができないので3から３より大きな数を引くとどうなるかもわかんなくなってしまうのでしょう。

その答えを聞いて私は「え？おまえさあ、３円持ってて５円借金したら儲かってるわけ？？？？？(笑)」と笑いながら聞きました。そうするとその子は「あれ？」という顔をしてしばらく考えていて、「あ、２円借金！」と答えられます。

でもしばらくしてまた同じような問題をやってみると、やっぱり足し算にしてみたりして、うまくできず、私が「え？お前さあ、……」の繰り返しでした。

そうやってしつこくやり続けていたら、それでも日もだいぶたつにつれて、だんだん間違えなくなってきます。そしてついには「儲け」と「借金」ではなく、単に「３-５」という数字だけでわかるようになりました。

何が効いたのかですが、マイナス5といった数字は彼らには最初ぴんと来なかったのですね。それに「儲け」とか「借金」といった具体的なイメージを与えて考えさせたわけです。そうすると、その具体的なイメージを手掛かりに「マイナス」ということを理解して正解することができるようになり、そしてそれを繰り返すことで、具体的なイメージがなくても、その背後にある計算の仕組みに気づくようになって、「3-5」でもできるようになっていったということになります。そうやって「マイナス」の概念を獲得していったともいえるでしょう。

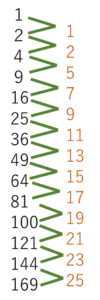
さて、そんな感じで思わず笑ってしまうような失敗を繰り返しながら、大げさに誉めたりからかったりしつつ、じっくりじっくり勉強を進めていきました。

もともと勉強ができないのでみんなからバカにされてしまって自信もなくなっていますし、そういうときはとにかく小さいことでも誉めるのが大事になります。「あれ？こんな俺にもできたりするのかな？」という気持ちをもってもらうことで「希望」という前向きな気持ちをもってもらうわけです。

ただ誉めるだけだと白々しく嘘っぽくなることもあるので、適当にからかったりしてちょっと挑発するのも効果大です。料理は砂糖だけだとダメで、ちょっと塩味も入れてあげないと甘味も生きてきません(笑)

そんなこんなでやりとりを楽しみながら進めるうち、あるときそのうちの一人がなにやらホワイトボードに数字を書いて一生懸命考えている様子でした。ちょうど自乗に関する話をやっているときだったのですが、図のような感じです。

ご覧いただいたらわかると思いますが、隣り合う二乗の数の差をとると、その差が２ずつ増えていくんですね。ちょっと詳しいことを忘れてしまったのですが、そこから彼はもうひとつ並んでいる数同士の関係を見つけて興奮していました。

一見でたらめに並んでいるように見える数の列の中に、安定した関係を見つける。それはまるで数学者が数学をやるようなことです。負の数の理解も危うかった彼が、自分の力で「数の秘密」を解き明かすまでになったのですね。この例だと数列という数学上の考え方にも結び付いていくような「発見」を彼は独力でやったわけです。

そんな風に勉強していって、受験前にはなんとか解の公式とか因数分解まではこなすようになって高校に行きました。さすがに自分で解の公式を導き出すところまでは力が及びませんでしたが、まあそれでも「変数」という抽象的な数の扱いも理解したわけですし（※）、最初の頃を考えれば彼らとしては大したものです。

……という風に、彼らは単に「形」をわけもわからず丸暗記したのではなく、試行錯誤しながらその背後にある仕組みを理解する方向へと進んでいったのです。暗記と試行錯誤の違いは何か、といえば、暗記には「思考」が要りません。それに対して「試行錯誤」というのは、ダジャレじゃないですが、そのこと自体が「思考」の一部なのです(※※)。

以前「失敗って大事」という記事を書きましたが、なぜ失敗が大事かというと、それは「試行錯誤」によってその課題の背後に隠れた意味を自分で発見するためのプロセスだからです。それこそが「思考」の力だというわけです。

さて、ここで視点をちょっと変えてみましょう。ここまでは「子どもが新しい課題をこなせるようになる」というプロセスを算数や数学を例に説明してみました。今度は子どもではなく、子どもを支援するスタッフについて考えてみます。「スタッフが新しい課題をこなせるようになる」プロセスということです。

スタッフにとっての新しい課題というのは、「子どもが新しい課題をこなせるように」支援することです。でもそれがうまくいかない。そういうときはどうしたらいいのか。それはスタッフ自身が「試行錯誤」することです。試行錯誤ですから失敗もたくさんします。その失敗の中で、「なぜ失敗するのか」を考える。あるいは「なぜ子どもが理解できないか」を考える。そこに進んでいくのか、その前に立ち止まってしまうのかで結果が180度変わるわけです。

「試行錯誤」を避けようとされる人は、すぐに誰かに「答え」を求める傾向があります。「こうやってもうまくいかないんだけど、どうしたらいいですか？」と「答え」を求める。もちろんそれがヒントになって、「理由」を考えられるのならそれは大切な質問です。けれども往々にしてそこで教えられたやり方を、ただ「形」だけ「暗記」することになってしまいやすい。

当然そうなると「応用」が利かなくなります。だから教えられたそのやり方でうまくいかなくなると、もうお手上げになって、また「今度はどうしたらいいんですか？」と聞くしかなくなる。その繰り返しでは切りがありません。「試行錯誤」の中で、自分で答えを見つけていく姿勢がない限り、永遠にその連続です。

これは、自分が教えようとしている子どもが置かれている状況と同じなわけですね。「なぜそうなるの？」という問いがないままただ答えだけを教えられる。それではいつまでたっても自分で考えて理解する力が育ちません。そういう暗記ばかりやらされて失敗を続けて、いやになるのは当然です。そうやって子どもの方が嫌がるようになると、スタッフはますます自信がなくなったり、腹を立てて子どもを責めたりするようになる。

では子どもにとってもスタッフ自身にとってもこの不毛なパターンを抜けて前に進むにはどうしたらいいでしょうか？

基本として大事な態度は、子どもができないとき、「できない子だ！」と子どもに責任をかぶせてしまわないことだと私は思います。「ピアジェのすごいところ」に書いたように、子どもができないにはできない理由があります。支援する側はその理由を探ることが必要なのです。「この子はこの課題をどうしてわからないのかな？」と考えてみること。わからない理由を探ることです。

さらにそこから「なんで自分はわかるんだろう？」とむしろ自分がわかってしまうことが不思議なくらいに感じられるようになったら、これは大したものです。頭のいい人が必ずしも教えるのがうまいとは限らないのは、そこの問題が絡んでいます。自分はわかってしまうので、わからない子の気持ちがわからない。なぜわからないのかがわからない。それは言葉を変えると「自分がどうしてそれがわかっているのか」がわかっていないことでもあります。だからわからない子に教えるのが下手になるのです。

私は算数や中学生くらいの簡単な数学ならまあわりと子どもに伝わりやすいように教えられる方ですが、それは私自身が数学がとても苦手だからだと思っています。わかんないからどうしてわかんないのかも考えますし、子どもがどういうところでわかんなくなるかがなんとなくわかる。だからわからない子に教えやすくなるのですね。

ということは、上手に教えるには、自分が「わかっているつもり」にならずに、「え？なんでそうなるの？」と自分自身考え直してみる癖をつけることが必要ということにもなるでしょうか。ある意味「そんなの当たり前じゃない」とわかったように賢くなっている自分を捨てて、「ばかになる」ことが大事(笑)

一番だめなのは「わからない相手がバカなんだ！」で終わってしまう態度です。「わからない相手がなぜわからないのかわからない自分がバカなんだ」というくらいに謙虚になった方がいいんだと思います。

そうやって子どもと一緒に「あれ？なんでこうなるんだろうね？むつかしいねえ」と言い合えるようになると、ずいぶん状況が変わってくるだろうと思います。そして「ああかなあ、こうかなあ」と一緒に子どもと「試行錯誤」してみる。そうやって自分も子どものようになって考えていくと、それまで単に当たり前で済ませていたことについて、意外と自分にも新しい面白い発見があるものです。

時には大人の方がわざと間違えて見せて、「これでいいのかなあ？」と言ってみたりするのも面白いです。そうやって「正解を覚えさせる」のではなく、「一緒に迷いながら進む」ことを「楽しむ」のが一番いいんだと思います。

「子どもに先生役を」に紹介したヒオ先生の話も、「当たり前」を覚えこませるのではなくて、わざとそれをひっくり返して見せて「子どもに考えさせる、判断させる」遊びをやる話です。そういう遊びが、ただ訳もわからず「正解」を押し付けられるしんどさから解き放たれて子どもを生き生きとさせ、子どもに自分で考える力を育てるのですね。

そういう生き生きしたやりとりの中で子どもと課題に向き合っていくとき、それが同時に「子どもを理解する」力を支援者の側に育てることでもあるというわけです。

※　変数の意味を理解させるときには、最初は「中に数が隠れている箱」のイメージを使うと分かりやすいことが多いですね。これも「x」と書かれても抽象的過ぎてピンとこないけど、「何かそこに数字が隠れているんだ」と図にして具体的にイメージさせてみると分かりやすくなる。
もちろんその次のステップとしては、「x」の中身がどんどん変化していく、ということを理解する必要が出てきます。それでないと「関数」が理解できません。グラフはその関数を直観的に理解させてくれる大事なツールになります。
いずれも療育支援でもよくつかわれる「視覚化」というテクニックの一つとも言えます。そうやってだんだんと具体的な「もの」から抽象的な「関係」へと理解が進んでいく、というのが数学の大事な展開になります。
やがて数学はその有力な発展の一つとして、「関係」を成り立たせている操作のシステムの解明にも進んでいき、構造主義数学に展開し、形式論理学と融合していくことになるようです。
ピアジェは知能の本質を対象変換の操作の構造と考え、そして構造はその操作が組み合わさって動的な均衡状態を生み出しうるようになったものと考えましたが、その知能の発達の最終段階として考えた論理数学的知能というのは、数学的な変換操作と論理的な変換操作の両方の基礎にある知能ということになります。

※※　もちろん丸暗記が必要なものもたくさんあります。例えば数字の形は「なんでこう書くのか」という理由を考える前に、まずはその形や書き方を丸暗記する必要がありますよね。それを使って数の理解が進むわけなので、いってみればそれは理解のための材料のようなものです。九九も暗記する必要がありますが、ただその結果を使えるには掛け算の意味は理解しておかなければなりません。九九はそういう掛け算の意味を知った上で、それを効率よく使いこなすための公式のようなものです。